Bài tập về tìm giá trị lớn số 1 (GTLN) cùng giá trị bé dại nhất (GTNN) của hàm số không phải là dạng toán khó, không dừng lại ở đó dạng toán này nhiều khi xuất hiện trong đề thi giỏi nghiệp THPT. Vì vậy những em cần nắm vững để chắc chắn đạt điểm tối đa nếu tất cả dạng toán này.
Bạn đang xem: Tìm giá trị lớn nhất nhỏ nhất của hàm số
Vậy biện pháp giải so với các dạng bài tập tìm giá chỉ trị lớn nhất (GTLN) với giá trị nhỏ nhất (GTNN) của hàm số (như hàm số lượng giác, hàm số chứa căn,...) bên trên khoảng khẳng định như gắng nào? chúng ta cùng tìm hiểu qua nội dung bài viết dưới đây.
I. Kim chỉ nan về GTLN và GTNN của hàm số
• Cho hàm số y = f(x) khẳng định trên tập D ⊂ R.
- nếu tồn tại một điểm x0 ∈ X làm thế nào cho f(x) ≤ f(x0) với đa số x ∈ X thì số M = f(x0) được call là giá trị lớn nhất của hàm số f trên X.
Ký hiệu:
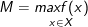
- nếu như tồn tại một điểm x0 ∈ X làm thế nào cho f(x) ≥ f(x0) với đa số x ∈ X thì số m = f(x0) được gọi là giá chỉ trị nhỏ tuổi nhất của hàm số f bên trên X.
Ký hiệu:
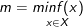
II. Các dạng bài tập tìm GTLN và GTNN của hàm số và phương pháp giải
° Dạng 1: Tìm giá bán trị lớn số 1 và quý hiếm của nhất của hàm số bên trên đoạn
- nếu hàm số f(x) tiếp tục trên đoạn
* phương thức giải:
- cách 1: Tính f"(x), giải phương trình f"(x) = 0 ta được các điểm cực trị x1; x2;... ∈
- cách 2: Tính những giá trị f(a); f(x1); f(x2);...; f(b)
- bước 3: Số bự nhất trong số giá trị trên là GTLN của hàm số f(x) bên trên đoạn
• Chú ý: Khi bài toán không chỉ là rõ tập X thì ta gọi tập X đó là tập xác minh D của hàm số.
* ví dụ 1 (Bài 1 trang 23-24 SGK Giải tích 12): Tìm GTLN với GTNN của hàm số:
a) y = x3 - 3x2 - 9x + 35 trên các đoạn <-4; 4> cùng <0; 5>
b) y = x4 - 3x2 + 2 trên các đoạn <0; 3> cùng <2; 5>
° Lời giải:
- Để ý vấn đề trên có 2 hàm vô tỉ, một hàm hữu tỉ với 1 hàm gồm chứa căn. Chúng ta sẽ tìm GTLN và GTNN của các hàm này.
Xem thêm: Chiếc Xe Đạp Điện Tương Lai Của Em, Khám Phá Xu Hướng Xe Đạp Điện Cho Tương Lai
a) y = x3 - 3x2 - 9x + 35 trên các đoạn <-4; 4> với <0; 5>
+) Xét hàm số trên tập D = <-4; 4>
- Ta có: y" = 3x2 - 6x - 9 = 0 ⇔ x = –1 (∈ D) hoặc x = 3 (∈ D) nên:
y(-4) = (-4)3 - 3(-4)2 - 9(-4) + 35 = -41
y(-1) = (-1)3 - 3(-1)2 - 9(-1) + 35 = 40
y(3) = (3)3 - 3(3)2 - 9(3) + 35 = 8
y(4) = (4)3 - 3(4)2 - 9(4) + 35 = 15
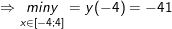
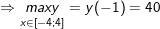
+) Xét hàm số trên tập D = <0; 5>
- Ta có: y" = 3x2 - 6x - 9 = 0 ⇔ x = –1 (∉ D) hoặc x = 3 (∈ D) nên:
y(0) = 35; y(3) = 8; y(5) = 40.
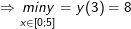
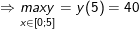
b) y = x4 - 3x2 + 2 trên những đoạn <0; 3> với <2; 5>
- Ta có:
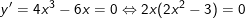
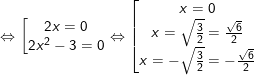
+) Xét D = <0; 3>, có:

- Ta có:
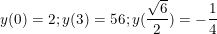
- Vậy
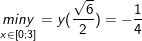
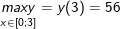
+) Xét D = <2; 5>, có:
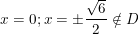
- Ta có:
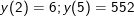
- Vậy
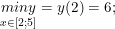
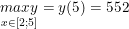
* lấy ví dụ như 2 (Câu c bài xích 1 trang 23-24 SGK Giải tích 12): Tìm GTLN cùng GTNN của hàm số hữu tỉ:
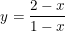
° Lời giải
- Ta có:
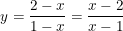
- Tính:
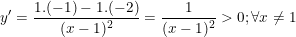
+) với D = <2; 4> có: y(2) = 0; y(4) = 2/3
- Vậy
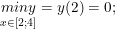
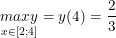
+) cùng với D = <-3; -2> có: y(-3) = 5/4; y(-2) = 4/3
- Vậy
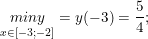
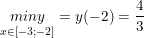

* lấy ví dụ 3 (Câu d bài bác 1 trang 23-24 SGK Giải tích 12): Tìm GTLN cùng GTNN của hàm số cất căn:
trên đoạn <-1; 1>.
° Lời giải:
d) trên đoạn <-1; 1>.
- Ta có: TXĐ:
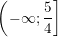
- Xét tập D = <-1;1> có:
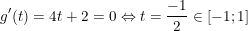
- Ta có:
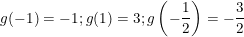
- Vậy hàm số g(t) đạt giá bán trị lớn nhất bằng 3 khi:
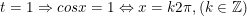
và đạt giá bán trị bé dại nhất bởi -3/2 khi:
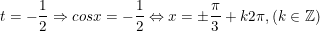
* ví dụ như 5 : Tìm GTLN cùng GTNN của hàm số lượng giác: f(x) = cos2x + 2sinx - 3 với
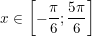
° Lời giải:
- Từ công thức tất cả cos2x = 1 - 2sin2x, ta có:
f(x) = 1 - 2sin2x + 2sinx - 3 = -2sin2x + 2sinx - 2
- Đặt t = sinx; ta có:

- Ta có: g(t) = -2t2 + 2t - 2
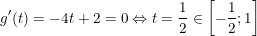
- Tính được:
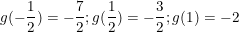
- Vậy:
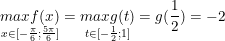
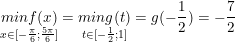
° Dạng 2: Tìm giá bán trị lớn số 1 và quý giá của nhất của hàm số trên khoảng chừng (a;b).
* phương thức giải:
• Để tìm GTLN với GTNN của hàm số bên trên một khoảng tầm (không buộc phải đoạn, tức X ≠
- cách 1: tìm tập xác minh D và tập X
- bước 2: Tính y" với giải phương trình y" = 0.
- cách 3: Tìm những giới hạn khi x dần dần tới các điểm đầu khoảng chừng của X.
- cách 4: Lập bảng đổi mới thiên (BBT) của hàm số bên trên tập X
- bước 5: phụ thuộc BBT suy ra GTLN, GTNN của hàm số bên trên X.
* ví dụ như 1: Tìm giá chỉ trị lớn nhất, nhỏ nhất của hàm số sau:
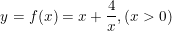
° Lời giải:
- Ta có: D = (0; +∞)
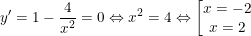
- Ta thấy x = -2 ∉ (0; +∞) đề nghị loại, phương diện khác:
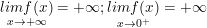
- Ta bao gồm bảng trở nên thiên:
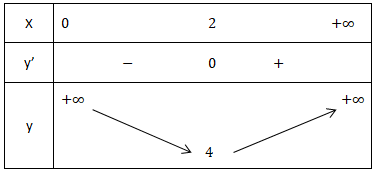
- từ BBT ta kết luận:
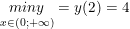
* lấy một ví dụ 2: tìm GTLN, GTNN của hàm số:
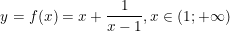
° Lời giải:
- TXĐ: R1
- Ta có:
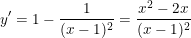
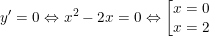
- Ta thấy x = 0 ∉ (1; +∞) phải loại, mặt khác:
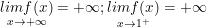
- Ta có bảng biến thiên sau:
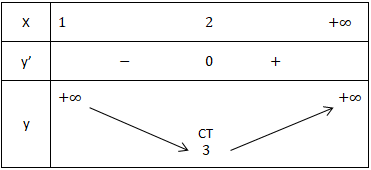
- tự bảng biến hóa thiên ta kết luận:

Như vậy, các em để ý để tìm giá chỉ trị lớn số 1 và giá trị bé dại nhất của hàm số ta hoàn toàn có thể sử một trong hai cách thức là lập bảng trở nên thiên hoặc ko lập bảng phát triển thành thiên. Tùy vào mỗi việc mà họ lựa chọn phương pháp phù hợp nhằm giải.
Thực tế thì với việc tìm GTLN, GTNN trên đoạn chúng ta thường ít khi thực hiện pp lập bảng thay đổi thiên. Lập bảng phát triển thành thiên thường thực hiện cho việc tìm GTLN cùng GTNN bên trên khoảng.
Ngoài ra, vấn đề về GTLN với GTNN còn được áp dụng để biện luận nghiệm của phương trình (hoặc bất phương) trình dạng f(x) = g(m) (hay f(x)